Offset Quaternary Phase Shift Keying (OQPSK)

Introduction

Offset Quaternary Phase Shift Keying, OQPSK, is like QPSK except that the quadrature component is delay 1/2-symbol time relative to the in-phase component. This avoids phase trajectories through the origin which, in turn, is a good thing when a non-linear RF power amplifier is used. (See Rice, Section 5.4, pp. 260 - 265.) Because of its relationship to QPSK, the OQPSK constellation consists of four points equally spaced on a circle. In this exercise, you will design an OQPSK detector to process the data contained in the file oqpskdata.mat

Textbook References

Offset QPSK: Section 5.4 (pp. 260 - 265), full response pulse shapes: Section A.1 (pp. 673 - 676).

Specifications

normalized sample rate: 20 samples/symbol normalized carrier frequency: 0.3 cycles/sample carrier phase: 0 degrees average energy: 10 pulse shape: HS symbol clock offset: 0 input file oqpskdata.mat input message length: 63 symbols (126 bits or 18 ASCII characters)

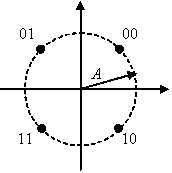Preliminary Design

Design the Detector

Design the detector, shown below, using blocks from the Simulink, DSP System, and Communications System Toolboxes.



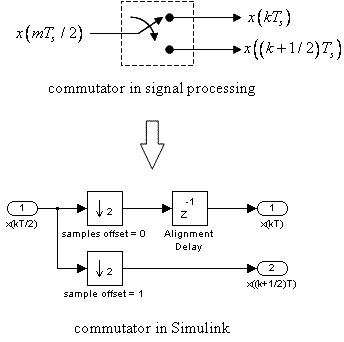
The matched filter outputs are downsampled to two samples/symbol (or one sample/bit) in synchronism with the symbols. The samples are commutated as shown. After commutation, the clock rate is one sample/symbol, the even- and odd-indexed samples appearing in parallel. Detection is based on the even-indexed samples from the I-channel and the odd-indexed samples from the Q-channel. The unused samples will be used for carrier phase synchronization as explained in the Simulink exercise on Carrier Phase Synchronization for OQPSK. More information on this structure is available in Section 5.4 of the text.

The system requires a commutator. The data samples arrive at the input at a rate equivalent to 2 samples/symbol and are output in two parallel streams at a symbol rate equivalent to 1 sample/symbol. The commutator may be constructed in Simulink using a pair of downsample blocks with different sample offsets and a delay as shown below. (The delay is required to properly align the even- and odd-indexed samples.)

Test the Detector Design

You should test the detector you designed by constructing a modulator to produce a test signal. The following procedure steps you through this design process:

1. Design the modulator shown below to meet the above specifications except make the input the four symbol sequence 0 2 1 3.
   
   
   
   


2. Connect the output of your modulator to the input of your detector.


3. Connect the output of your detector to a To Workspace block (be sure to open the Properties Dialog Window and set the Save format to matrix) and a Scope block.


4. Set the simulation parameters as follows:

   Simulation Time

   Start Time:	0.0
   Stop Time:	(1+4)*8

   Solver Options

   Type:	Fixed-step
   Solver:	discrete (no continuous states)
   Fixed step size:	auto

   Tasking and sample time options

   Periodic sample time constraint:	Unconstrained
   Tasking mode for periodic sample times:	SingleTasking



5. Run the simulation and plot the demodulator input and the matched filter output on the same set of axes. The simulation produces 6 downsampled matched filter outputs pairs -- the last 4 correspond to the sequence (0 2 1 3). Check the values in the workspace to see if they agree with input sequence (0 2 1 3).


6. Adjust the offset of the Downsample block to obtain the proper values.

Exercise

1. Replace the modulator blocks with the From File block and set the Filename to oqpskdata.mat and the sample time to 1.


2. Set the simulation parameters as follows:

   Simulation Time

   Start Time:	0.0
   Stop Time:	(1+63)*20

   Solver Options

   Type:	Fixed-step
   Solver:	discrete (no continuous states)
   Fixed step size:	auto

   Tasking and sample time options

   Periodic sample time constraint:	Unconstrained
   Tasking mode for periodic sample times:	SingleTasking



3. Run the simulation.


4. The detector produces 65 symbol estimates. The last 63 of these correspond to 18 7-bit ASCII characters. Determine the message using either your Matlab script or an ASCII Table.


5. Plot the eye diagram and signal space projections.