Digital Communications: A Discrete-Time Approach
by Michael Rice

Carrier Phase Synchronization for Offset QPSK Using Differential Encoding/Decoding
Introduction
In the previous OQPSK Simulink Exercise the phase of the unmodulated carrier was assumed known. Unfortunately, this is not the case in practice. The carrier phase is unknown and must be extracted from the received signal using a carrier phase recovery subsystem. In this exercise, you will design a PLL-based carrier phase recovery subsystem for OQPSK which will be used to process OQPSK modulated data contained in the file oqpskcrdata.mat The carrier phase error detector for non-offset QPSK possessed a 90-degree phase ambiguity. For Offset-QPSK, the carrier phase error detector possesses a 180-degree phase ambiguity. However, for Offset-QPSK, an additional ambiguity exists. It will not be known which sample index corresponds to the inphase component and which sample corresponds to the delayed quadrature component. Thus a differential encoder/encoder must account for this additional ambiguity. In this exercise, such a differential encoding is used.Textbook References
Offset QPSK: Section 5.4 (pp. 260 - 265), discrete-time realizations: Section 5.3.2 (pp. 256 - 260), full response pulse shapes: Section A.1 (pp. 673 - 676), discrete-time PLL: Section C.2 (pp. 732 - 747), carrier phase synchronization for OQPSK: Section 7.5 (pp. 382 - 391), differential encoding for phase ambiguity resolution for OQPSK: Section 7.7.2 (pp. 405 - 409).Specifications
 |
|
Notes
- The data bits are differentially encoded.
Let the data bits be b(1) b(2) b(3) b(4) ... b(n) b(n+1) ...
where the Matlab convention of starting with index 1 (instead of index 0) has been used.
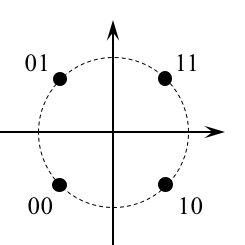
Without differential encoding, data bits b(1) and b(2) select the first
OQPSK symbol, data bits b(3) and b(4) select the second OQPSK symbol,
and so on.
Let the differentially encoded bits be
d(1) d(2) d(3) d(4) ... d(n) d(n+1) ... where the differential encoding rule is
d(n) = b(n) XOR ~d(n-1)
d(n+1) = b(n+1) XOR d(n)
for odd values of n where ~d(n-1) means the logical compliment of d(n-1). The differentially encoded bits are now used to select the OQPSK symbol as illustrated by the bit-to-symbol mapping above: d(1) and d(2) select the first OQPSK symbol, d(3) and d(4) select the second OQPSK symbol, and so on. - The detector requires a differential decoder.
The differential decoder operates on the estimated bit sequence
d(1) d(2) d(3) d(4) ... d(n) d(n+1) ....
The differential decoding rule is
b(n) = d(n) XOR ~d(n-1)
b(n+1) = d(n+1) XOR d(n)
for odd values of n. As before ~d(n-1) means the logical complement of d(n-1).
Design the Detector
Design the detector, shown below, using blocks from the Simulink, DSP System, and Communications System Toolboxes. I recommend you start with your OQPSK detector designed for the OQPSK Simulink Exercise and make changes as necessary.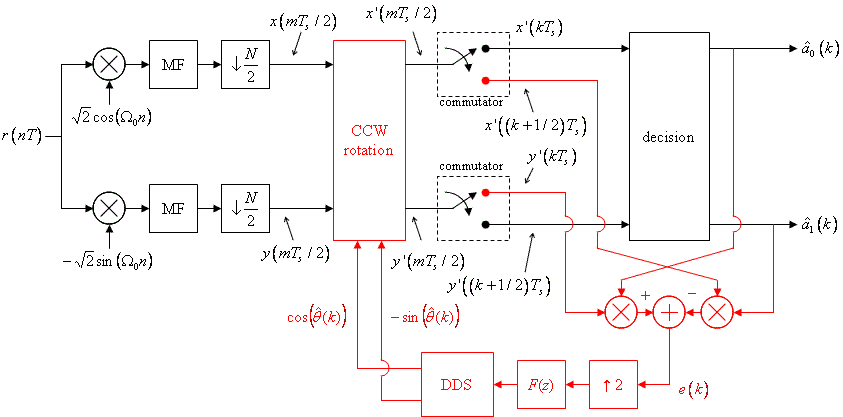
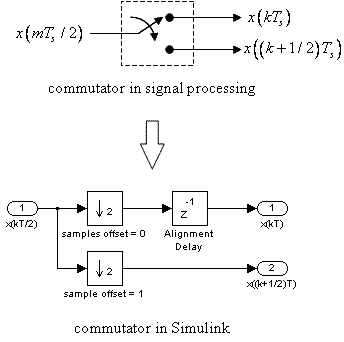
Note that the system requires a commutator. The data samples arrive at the input at a rate equivalent to 2 samples/symbol and are output in two parallel streams at a symbol rate equivalent to 1 sample/symbol. The commutator may be constructed in Simulink using a pair of downsample blocks with different sample offsets and a delay as shown below. (The delay is required to properly align the even- and odd-indexed samples.)
Design the loop filter to create a second order loop to the following specifications: closed-loop equivalent noise bandwidth = 0.01 (normalized to the symbol rate), damping factor = 0.7071. Note that the loop filter and DDS operate at 2 samples/symbol. Because the phase detector operates at 1 sample/symbol, the phase detector output is upsampled by 2 (by inserting a zero) prior to being filtered by the loop filter.
Exercise
- For the detector input, use the From File block and set the Filename to qpskcrdedata.mat and set the sample time to 1.
-
Set the simulation parameters as follows:
Simulation Time Start Time: 0.0 Stop Time: (8+231+2)*20*3 Solver Options Type: Fixed-step Solver: discrete (no continuous states) Fixed step size: auto Tasking and sample time options Periodic sample time constraint: Unconstrained Tasking mode for periodic sample times: SingleTasking - Run the simulation.
- The detector produces 724 symbol estimates. Convert the symbols to 1448 bits and apply the differential decoding rule defined above.
- Even though the SYNC and DATA fields are repeated three times, the PLL does not lock until part way through the sample sequence. To find the data bits, look for the 16-bit SYNC pattern in the differential decoder output. The 462 bits following the SYNC pattern correspond to 66 7-bit ASCII characters.
- Determine the message using either your Matlab script or an ASCII Table.
- Plot the phase error (loop filter output) and use this plot to estimate how long (measured in bits) it took your PLL to lock.
- Plot the eye diagram and signal space projections.
Brigham Young University - Provo |
Fulton College of Engineering |
The Church of Jesus Christ of Latter-day Saints
Department of Electrical and Computer Engineering, BYU, Provo, UT 84602 - (801)422-4012 - Copyright 2009. All Rights Reserved
Department of Electrical and Computer Engineering, BYU, Provo, UT 84602 - (801)422-4012 - Copyright 2009. All Rights Reserved