Carrier Phase Synchronization for QPSK Using the Unique Word

Introduction

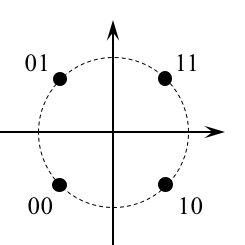
In the previous QPSK Simulink Exercise the phase of the unmodulated carrier was assumed known. Unfortunately, this is not the case in practice. The carrier phase is unknown and must be extracted from the received signal using a carrier phase recovery subsystem. In this exercise, you will design a PLL-based carrier phase recovery subsystem for QPSK which will be used to process QPSK modulated data contained in the file qpskcruwdata.mat

To deal with the 90-degree phase ambiguity of the PLL-based carrier phase synchronizer, this exercise uses the unique word (UW) method. In the UW method, the symbol decisions are searched for the four versions of the UW that correspond to the four possible constellation rotations defined by the phase ambiguity. Once the UW has been found, the phase ambiguity is known and can be corrected.

Textbook References

M-ary QAM: Section 5.3, discrete-time realizations: Section 5.3.2, partial response pulse shapes: Section A.2, discrete-time PLL: Section C.2, carrier phase synchronization for QPSK: Section 7.2, unique word for phase ambiguity resolution for QPSK: Section 7.7.1.

Specifications

	normalized sample rate: 8 samples/bit normalized carrier frequency: 0.3 cycles/sample carrier phase: unknown average energy: 2 pulse shape: SRRC (50% excess bandwidth, span = 12 symbols) symbol clock offset: 0 input file qpskcruwdata.mat phase ambiguity resolution unique word: UW = 1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1 input message length: 1211 symbols (2422 bits or 346 ASCII characters)
	the data format is shown below The packet is repeated 4 times to allow your PLL to acquire and lock.

Design the Detector

Design the detector, shown below, using blocks from the Simulink, DSP System, and Communications System Toolboxes. I recommend you start with the detector from the QPSK Simulink Exercise and make changes as necessary.



Design the loop filter to create a second order loop to the following specifications: closed-loop equivalent noise bandwidth = 0.02 (normalized to the symbol rate), damping factor = 0.7071.

Exercise

1. For the detector input, use the From File block and set the Filename to qpskcruwdata.mat and set the sample time to 1.


2. Set the simulation parameters as follows:
   
   

   Simulation Time
   Start time: 0.0	Stop time: (12+(8+1211)*4)*8-1
   Solver selection
   Type: Fixed-step	Solver: discrete (no continuous states)



3. Run the simulation.


4. The detector produces 4888 symbol estimates. Even though the UW and DATA fields are repeated four times, the PLL does not lock until part way through the sample sequence.


5. To find the data symbols, look for the 16-bit (8 symbol) UW pattern in the detector output. If you find it (and you may find it more than once), the 1211 symbols following the UW correspond to 346 7-bit ASCII characters.


6. If you cannot find the 16-bit (8 symbol) UW pattern in the detector output, rotate the UW by 90 degrees and search of the rotated UW. If you find it, de-rotate the detector output by 90 degrees (i.e., rotate by -90 degrees). The 1211 de-rotated symbols following the rotated UW correspond to 346 7-bit ASCII characters.


7. If you still do not find it, repeat the previous step for a 180 degree rotation.


8. If you still do not find it, repeat the previous step for a 270 degree rotation.


9. Determine the message using either your Matlab script or an ASCII Table.


10. Plot the phase error (loop filter output) and use this plot to estimate how long (measured in bits) it took your PLL to lock.


11. Plot the eye diagram and signal space projections.