Quaternary Phase Shift Keying (QPSK)

Introduction

Quaternary Phase Shift Keying, QPSK, is one of the most popular digital carrier modulations in use today. The QPSK signal set consists of four waveforms that differ in phase: they are each 90-degrees apart. For this reason, the QPSK constellation consists of four points equally spaced on a circle. In this exercise, you will design QPSK detector to process the data contained in the file qpskdata.mat

Textbook References

M-ary QAM: Section 5.3, discrete-time realizations: Section 5.3.2, partial response pulse shapes: Section A.2.

Specifications

normalized sample rate: 8 samples/symbol normalized carrier frequency: 0.25 cycles/sample carrier phase: 0 degrees average energy: 9 pulse shape: SRRC (50% excess bandwidth, span = 12 symbols) symbol clock offset: 0 input file qpskdata.mat input message length: 602 symbols (1204 bits or 172 ASCII characters)

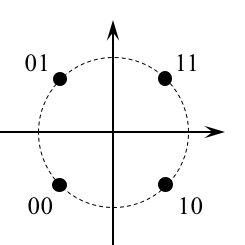Preliminary Design

Design the Detector

Design the detector, shown below, using blocks from the Simulink, DSP System, and Communications System Toolboxes.

Test the Detector Design

Test the detector you designed by constructing a modulator to produce a test signal. The following procedure steps you through this design process:

1. Design the modulator shown below to meet the above specifications except make the input the four symbol sequence 0 2 1 3.
   
   
   
   


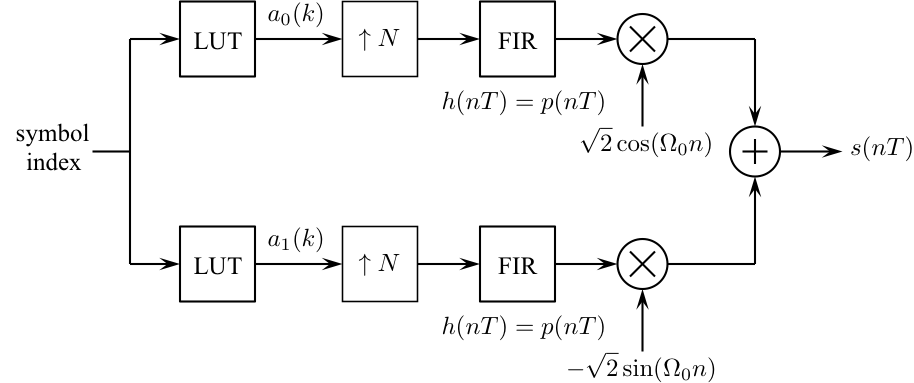
2. Connect the output of your modulator to the input of your detector.


3. Connect the output of your detector to a To Workspace block (be sure to open the Properties Dialog Window and set the Save format to matrix) and a Scope block.


4. Set the simulation parameters as follows:
   
   

   Simulation Time
   Start time: 0.0	Stop time: (12+4)*8-1
   Solver selection
   Type: Fixed-step	Solver: discrete (no continuous states)

   
   Note: the stop time is computed as follows: 12 = 2*(span/2) [the delay of the pulse shaping filter plus the delay of the matched filter]; 4 = the number of data symbols; 8 = the number of samples/symbol. We subtract because the start time is t = 0.0.


5. Run the simulation and plot the demodulator input and the matched filter output on the same set of axes. The simulation produces 16 downsampled matched filter outputs -- the last 4 correspond to the sequence (0 2 1 3). Check the values in the workspace to see if they agree with input sequence (0 2 1 3).


6. Examine the output of the Downsample block to see if the downsample operation is keeping the desired samples. Adjust the sample offset of the Downsample block to obtain the proper values.

Exercise

1. Replace the modulator blocks with the From File block and set the Filename to qpskdata.mat and the sample time to 1.


2. Set the simulation parameters as follows:
   
   

   Simulation Time
   Start time: 0.0	Stop time: (12+602)*8-1
   Solver selection
   Type: Fixed-step	Solver: discrete (no continuous states)



3. Run the simulation.


4. The detector produces 614 symbol estimates. The last 602 of these correspond to 172 7-bit ASCII characters. Determine the message using either your Matlab script or an ASCII Table.


5. Plot the eye diagram and signal space projections.